电子书
教程
Python
友链
关于
资源
idea激活2021
方志朋的专栏

2 数据结构和算法面试题系列—二叉树

2019/06/26

这个系列是我多年前找工作时对数据结构和算法总结，其中有基础部分，也有各大公司的经典的面试题，最早发布在CSDN。现整理为一个系列给需要的朋友参考，如有错误，欢迎指正。本系列完整代码地址在 这里。

0 概述

在说二叉树前，先来看看什么是树。树中基本单位是结点，结点之间的链接，称为分支。一棵树最上面的结点称之为根节点，而下面的结点为子结点。一个结点可以有0个或多个子结点，没有子结点的结点我们称之为叶结点。

二叉树是指子结点数目不超过2个的树，它是一种很经典的数据结构。而二叉搜索树(BST)是有序的二叉树，BST需要满足如下条件：

  • 若任意结点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
  • 若任意结点的右子树不空，则右子树上所有节点的值均大于或等于它的根节点的值；(有些书里面定义为BST不能有相同值结点，本文将相同值结点插入到右子树)
  • 任意结点的左、右子树也分别为二叉查找树；

本文接下来会从定义，二叉搜索树的增删查以及二叉树的递归和非递归遍历进行整理。 下一篇文章会对二叉树相关的经典面试题进行全面解析，本文代码在 这里。

1 定义

我们先定义一个二叉树的结点，如下：

  typedef struct BTNode {
        int value;
        struct BTNode *left;
        struct BTNode *right;
    } BTNode;
    Java极客，javajike.com

其中 value 存储值，left 和 right 指针分别指向左右子结点。二叉搜索树跟二叉树可以使用同一个结构，只是在插入或者查找时会有不同。

2 基本操作

接下来看看二叉树和二叉查找树的一些基本操作，包括BST插入结点，BST查找结点，BST最大值和最小值，二叉树结点数目和高度等。二叉查找树(BST)特有的操作都在函数前加了 bst 前缀区分，其他函数则是二叉树通用的。

1) 创建结点

分配内存，初始化值即可。

  
    /**
     * 创建BTNode
     */
    BTNode *newNode(int value)
    {
        BTNode *node = (BTNode *)malloc(sizeof(BTNode));
        node->value = value;
        node->left = node->right = NULL;
        return node;
    }
    Java极客，javajike.com

2) BST 插入结点

插入结点可以用递归或者非递归实现，如果待插入值比根节点值大，则插入到右子树中，否则插入到左子树中。如下图所示(图来自参考资料1，2，3)：

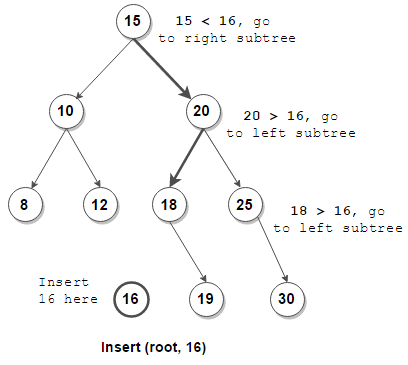
anshitixilieerchashujichu_1.png

  /**
     * BST中插入值，递归方法
     */
    /**
     * BST中插入结点，递归方法
     */
    BTNode *bstInsert(BTNode *root, int value)
    {
        if (!root)
            return newNode(value);
    
        if (root->value > value) {
            root->left = bstInsert(root->left, value);
        } else {
            root->right = bstInsert(root->right, value);
        }
        return root;
    }
    
    /**
     * BST中插入结点，非递归方法
     */
    BTNode *bstInsertIter(BTNode *root, int value)
    {
        BTNode *node = newNode(value);
    
        if (!root)
            return node;
    
        BTNode *current = root, *parent = NULL;
    
        while (current) {
            parent = current;
            if (current->value > value)
                current = current->left;
            else
                current = current->right;
        }
    
        if (parent->value >= value)
            parent->left = node;
        else
            parent->right = node;
    
        return root;
    }
    Java极客，javajike.com

3) BST 删除结点

删除结点稍微复杂一点，要考虑3种情况：

  • 删除的是叶子结点，好办，移除该结点并将该叶子结点的父结点的 left 或者 right 指针置空即可。

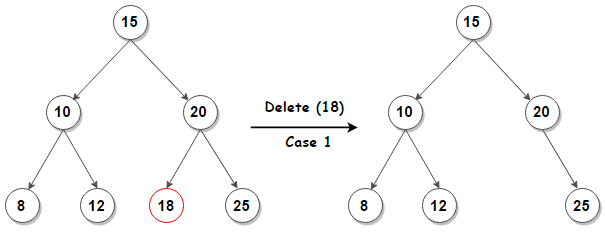
anshitixilieerchashujichu_2.png

  • 删除的结点有两个子结点，则需要找到该结点左子树的最大结点(使用后面的bstSearchIter 函数)，并将其值替换到待删除结点中，然后递归调用删除函数删除该结点左子树最大结点即可。

anshitixilieerchashujichu_3.png

  • 删除的结点只有一个子结点，则移除该结点并将其子结点的值填充到该删除结点即可(需要判断是左孩子还是右孩子结点)。

anshitixilieerchashujichu_4.png

  /**
     * BST中删除结点
     */
    BTNode *bstDelete(BTNode *root, int value)
    {
        BTNode *parent = NULL, *current = root;
        BTNode *node = bstSearchIter(root, &parent, value);
        if (!node) {
            printf("Value not found\n");
            return root;
        }
    
        if (!node->left && !node->right) {
            // 情况1：待删除结点是叶子结点
            if (node != root) {
                if (parent->left == node) {
                    parent->left = NULL;
                } else {
                    parent->right = NULL;
                }
            } else {
                root = NULL;
            }
            free(node);
        } else if (node->left && node->right) {
            // 情况2：待删除结点有两个子结点
            BTNode *predecessor = bstMax(node->left);
            bstDelete(root, predecessor->value);
            node->value = predecessor->value;
        } else {
            // 情况3：待删除结点只有一个子结点
            BTNode *child = (node->left) ? node->left : node->right;
            if (node != root) {
                if (node == parent->left)
                    parent->left = child;
                else
                    parent->right = child;
            } else {
                root = child;
            }
            free(node);
        }
        return root;
    }
    Java极客，javajike.com

4) BST 查找结点

注意在非递归查找中会将父结点也记录下来。

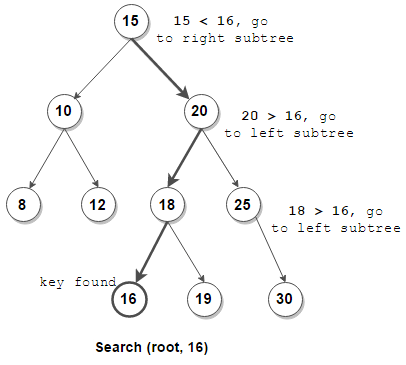
anshitixilieerchashujichu_5.png

  /**
     * BST查找结点-递归
     */
    BTNode *bstSearch(BTNode *root, int value)
    {
        if (!root) return NULL; 
    
        if (root->value == value) {
            return root;
        } else if (root->value > value) {
            return bstSearch(root->left, value);
        } else {
            return bstSearch(root->left, value);
        }
    }
    
    /**
     * BST查找结点-非递归
     */
    BTNode *bstSearchIter(BTNode *root, BTNode **parent, int value)
    {
        if (!root) return NULL;
    
        BTNode *current = root;
    
        while (current && current->value != value) {
            *parent = current;
            if (current->value > value)
                current = current->left;
            else
                current = current->right;
        }
    
        return current;
    }
    Java极客，javajike.com

5）BST 最小值结点和最大值结点

最小值结点从左子树递归查找，最大值结点从右子树递归找。

  /**
     * BST最小值结点
     */
    BTNode *bstMin(BTNode *root)
    {
        if (!root->left)
            return root;
    
        return bstMin(root->left);
    }
    
    /**
     * BST最大值结点
     */
    BTNode *bstMax(BTNode *root)
    {
        if (!root->right)
            return root;
    
        return bstMax(root->right);
    }
    
    Java极客，javajike.com

6）二叉树结点数目和高度

  /**
     * 二叉树结点数目
     */
    int btSize(BTNode *root)
    {
        if (!root) return 0;
        
        return btSize(root->left) + btSize(root->right) + 1;
    }
    
    /**
     * 二叉树高度
     */
    int btHeight(BTNode *root)
    {
        if (!root) return 0;
    
        int leftHeight = btHeight(root->left);
        int rightHeight = btHeight(root->right);
        int maxHeight = leftHeight > rightHeight ? leftHeight+1 : rightHeight+1;
        return maxHeight;
    }
    Java极客，javajike.com

3 二叉树遍历

递归遍历-先序、中序、后序、层序

二叉树遍历的递归实现比较简单，直接给出代码。这里值得一提的是层序遍历，先是计算了二叉树的高度，然后调用的辅助函数依次遍历每一层的结点，这种方式比较容易理解，虽然在时间复杂度上会高一些。

  /**
     * 二叉树先序遍历
     */
    void preOrder(BTNode *root)
    {
        if (!root) return;
    
        printf("%d ", root->value);
        preOrder(root->left);
        preOrder(root->right);
    }
    
    /**
     * 二叉树中序遍历
     */
    void inOrder(BTNode *root)
    {
        if (!root) return;
    
        inOrder(root->left);
        printf("%d ", root->value);
        inOrder(root->right);
    }
    
    /**
     * 二叉树后序遍历
     */
    void postOrder(BTNode *root)
    {
        if (!root) return;
    
        postOrder(root->left);
        postOrder(root->right);
        printf("%d ", root->value);
    }
    
    /**
     * 二叉树层序遍历
     */
    void levelOrder(BTNode *root)
    {
        int btHeight = height(root);    
        int level;
        for (level = 1; level <= btHeight; level++) {
            levelOrderInLevel(root, level);
        }
    }
    
    /**
     * 二叉树层序遍历辅助函数-打印第level层的结点
     */
    void levelOrderInLevel(BTNode *root, int level)
    {
        if (!root) return;
    
        if (level == 1) {
            printf("%d ", root->value);
            return;
        }
        levelOrderInLevel(root->left, level-1);
        levelOrderInLevel(root->right, level-1);
    }
    Java极客，javajike.com

非递归遍历-先序、中序、后序、层序

  • 非递归遍历里面先序遍历最简单，使用一个栈来保存结点，先访问根结点，然后将右孩子和左孩子依次压栈，然后循环这个过程。中序遍历稍微复杂一点，需要先遍历完左子树，然后才是根结点，最后才是右子树。
  • 后序遍历使用一个栈的方法postOrderIter()会有点绕，也易错。所以在面试时推荐用两个栈的版本postOrderIterWith2Stack()，容易理解，也比较好写。
  • 层序遍历用了队列来辅助存储结点，还算简单。
  • 这里我另外实现了一个队列 BTNodeQueue 和栈 BTNodeStack，用于二叉树非递归遍历。
  
    /*********************/
    /** 二叉树遍历-非递归 **/
    /*********************/
    /**
     * 先序遍历-非递归
     */
    void preOrderIter(BTNode *root)
    {
        if (!root) return;
    
        int size = btSize(root);
        BTNodeStack *stack = stackNew(size);
    
        push(stack, root);
        while (!IS_EMPTY(stack)) {
            BTNode *node = pop(stack);
            printf("%d ", node->value);
    
            if (node->right)
                push(stack, node->right);
    
            if (node->left)
                push(stack, node->left);
        }
        free(stack);
    }
    
    /**
     * 中序遍历-非递归
     */
    void inOrderIter(BTNode *root)
    {
        if (!root) return;
    
        BTNodeStack *stack = stackNew(btSize(root));
    
        BTNode *current = root;
        while (current || !IS_EMPTY(stack)) {
            if (current) {
                push(stack, current);
                current = current->left;
            } else {
                BTNode *node = pop(stack);
                printf("%d ", node->value);
                current = node->right;
            }
        }
        free(stack);
    }
    
    /**
     * 后续遍历-使用一个栈非递归
     */
    void postOrderIter(BTNode *root)
    {
        BTNodeStack *stack = stackNew(btSize(root));
        BTNode *current = root;
        do { 
            // 移动至最左边结点
            while (current) { 
                // 将该结点右孩子和自己入栈
                if (current->right) 
                    push(stack, current->right); 
                push(stack, current); 
      
                // 往左子树遍历
                current = current->left; 
            } 
      
            current = pop(stack); 
      
            if (current->right && peek(stack) == current->right) { 
                pop(stack);
                push(stack, current);
                current = current->right;
            } else { 
                printf("%d ", current->value); 
                current = NULL; 
            } 
        } while (!IS_EMPTY(stack)); 
    }
    
    /**
     * 后续遍历-使用两个栈，更好理解一点。
     */
    void postOrderIterWith2Stack(BTNode *root)
    {
        if (!root) return;
    
        BTNodeStack *stack = stackNew(btSize(root));
        BTNodeStack *output = stackNew(btSize(root));
    
        push(stack, root);
        BTNode *node;
    
        while (!IS_EMPTY(stack)) {
            node = pop(stack);
            push(output, node);
    
            if (node->left)
                push(stack, node->left);
    
            if (node->right)
                push(stack, node->right);
        }
    
        while (!IS_EMPTY(output)) {
            node = pop(output);
            printf("%d ", node->value);
        }
    }
    
    /**
     * 层序遍历-非递归
     */
    void levelOrderIter(BTNode *root)
    {
        if (!root) return;
    
        BTNodeQueue *queue = queueNew(btSize(root));
        enqueue(queue, root);
    
        while (1) {
            int nodeCount = QUEUE_SIZE(queue);
            if (nodeCount == 0)
                break;
    btHeight
            while (nodeCount > 0) {
                BTNode *node = dequeue(queue);
                printf("%d ", node->value);
    
                if (node->left)
                    enqueue(queue, node->left);
    
                if (node->right)
                    enqueue(queue, node->right);
    
                nodeCount--;
            }
            printf("\n");
        }
    }
    Java极客，javajike.com

参考资料

作者：ssjhust

来源：https://juejin.im/post/5ba3bb52e51d450e942f3031

本文为原创文章，转载请标明出处。
本文链接：http://blog.fangzhipeng.com/javainterview/2019/06/26/erchashu.html
本文出自方志朋的博客


（转载本站文章请注明作者和出处 方志朋-forezp）

宝剑锋从磨砺出，梅花香自苦寒来，用心分享，一起成长，做有温度的攻城狮!
   

Post Directory