这个系列是我多年前找工作时对数据结构和算法总结，其中有基础部分，也有各大公司的经典的面试题，最早发布在CSDN。现整理为一个系列给需要的朋友参考，如有错误，欢迎指正。本系列完整代码地址在这里。

0 概述

本文要描述的堆是二叉堆。二叉堆是一种数组对象，可以被视为一棵完全二叉树，树中每个结点和数组中存放该结点值的那个元素对应。树的每一层都是填满的，最后一层除外。二叉堆可以用于实现堆排序，优先级队列等。本文代码地址在这里。

1 二叉堆定义

使用数组来实现二叉堆，二叉堆两个属性，其中 LENGTH(A) 表示数组 A 的长度，而 HEAP_SIZE(A) 则表示存放在A中的堆的元素个数，其中 LENGTH(A) <= HEAP_SIZE(A)，也就是说虽然 A[0,1,...N-1] 都可以包含有效值，但是 A[HEAP_SIZE(A)-1] 之后的元素不属于相应的堆。

二叉堆对应的树的根为 A[0]，给定某个结点的下标 i ，可以很容易计算它的父亲结点和儿子结点。注意在后面的示例图中我们标注元素是从1开始计数的，而实现代码中是从0开始计数。

  #define PARENT(i) ( i > 0 ? (i-1)/2 : 0)
    #define LEFT(i) (2 * i + 1)
    #define RIGHT(i) (2 * i + 2)
    Java极客，javajike.com

注：堆对应的树每一层都是满的，所以一个高度为 h 的堆中，元素数目最多为 1+2+2^2+...2^h = 2^(h+1) - 1(满二叉树)，元素数目最少为 1+2+...+2^(h-1) + 1 = 2^h。由于元素数目 2^h <= n <= 2^(h+1) -1，所以 h <= lgn < h+1，因此 h = lgn 。即一个包含n个元素的二叉堆高度为 lgn 。

2 保持堆的性质

本文主要建立一个最大堆，最小堆原理类似。为了保持堆的性质，maxHeapify(int A[], int i) 函数让堆数组 A 在最大堆中下降，使得以 i 为根的子树成为最大堆。

  void maxHeapify(int A[], int i, int heapSize)
    {
        int l = LEFT(i);
        int r = RIGHT(i);
    
        int largest = i;
    
        if (l <= heapSize-1 && A[l] > A[i]) {
            largest = l;
        }
    
        if (r <= heapSize-1 && A[r] > A[largest]) {
            largest = r;
        }
    
        if (largest != i) { // 最大值不是i，则需要交换i和largest的元素，并递归调用maxHeapify。
            swapInt(A, i, largest);
            maxHeapify(A, largest, heapSize);
        }
    }
    Java极客，javajike.com

在算法每一步里，从元素 A[i] 和 A[left] 以及 A[right] 中选出最大的，将其下标存在 largest 中。如果 A[i] 最大，则以 i 为根的子树已经是最大堆，程序结束。
否则，i 的某个子结点有最大元素，将 A[i] 与 A[largest] 交换，从而使i及其子女满足最大堆性质。此外，下标为 largest 的结点在交换后值变为 A[i]，以该结点为根的子树又有可能违反最大堆的性质，所以要对该子树递归调用maxHeapify()函数。

当 maxHeapify() 函数作用在一棵以 i 为根结点的、大小为 n 的子树上时，运行时间为调整A[i]、A[left]、A[right] 的时间 O(1)，加上对以 i 为某个子结点为根的子树递归调用 maxHeapify 的时间。i 结点为根的子树大小最多为 2n/3(最底层刚好半满的时候)，所以可以推得 T(N) <= T(2N/3) + O(1)，所以 T(N)=O(lgN)。

下图是一个运行 maxHeapify(heap, 2) 的例子。A[] = {16, 4, 10, 14, 7, 9, 3, 2, 8, 1}，堆大小为 10。

3 建立最大堆

我们可以知道，数组 A[0, 1, ..., N-1] 中，A[N/2, ..., N-1] 的元素都是树的叶结点。如上面图中的 6-10 的结点都是叶结点。每个叶子结点可以看作是只含一个元素的最大堆，因此我们只需要对其他的结点调用 maxHeapify() 函数即可。

  void buildMaxHeap(int A[], int n)
    {
        int i;
        for (i = n/2-1; i >= 0; i--) {
            maxHeapify(A, i, n);
        }
    }
    Java极客，javajike.com

之所以这个函数是正确的，我们需要来证明一下，可以使用循环不变式来证明。

循环不变式：在for循环开始前，结点 i+1、i+2...N-1 都是一个最大堆的根。

初始化：for循环开始迭代前，i = N/2-1, 结点 N/2, N/2+1, ..., N-1都是叶结点，也都是最大堆的根。

保持：因为结点 i 的子结点标号都比 i 大，根据循环不变式的定义，这些子结点都是最大堆的根，所以调用 maxHeapify() 后，i 成为了最大堆的根，而 i+1, i+2, ..., N-1仍然保持最大堆的性质。

终止：过程终止时，i=0，因此结点 0, 1, 2, ..., N-1都是最大堆的根，特别的，结点0就是一个最大堆的根。

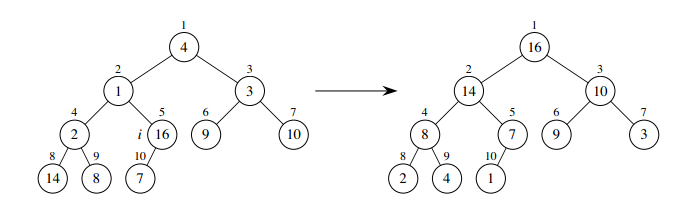
虽然每次调用 maxHeapify() 时间为 O(lgN)，共有 O(N) 次调用，但是说运行时间是 O(NlgN) 是不确切的，准确的来说，运行时间为 O(N)，这里就不证明了，具体证明过程参见《算法导论》。

4 堆排序

开始用 buildMaxHeap() 函数创建一个最大堆，因为数组最大元素在 A[0]，通过直接将它与A[N-1] 互换来达到最终正确位置。去掉 A[N-1]，堆的大小 heapSize 减1，调用maxHeapify(heap, 0, --heapSize) 保持最大堆的性质，直到堆的大小由N减到1。

  void heapSort(int A[], int n)
    {
        buildMaxHeap(A, n);
        int heapSize = n;
        int i;
        for (i = n-1; i >= 1; i--) {
            swapInt(A, 0, i);
            maxHeapify(A, 0, --heapSize);
        }
    }
    Java极客，javajike.com

5 优先级队列

最后实现一个最大优先级队列，主要有四种操作，分别如下所示：

insert(PQ， key)：将 key 插入到队列中。
maximum(PQ): 返回队列中最大关键字的元素
extractMax(PQ)：去掉并返回队列中最大关键字的元素
increaseKey(PQ, i, key)：将队列 i 处的关键字的值增加到 key

这里定义一个结构体 PriorityQueue 便于操作。

  typedef struct PriorityQueue {
        int capacity;
        int size;
        int elems[];
    } PQ;
    Java极客，javajike.com

最终优先级队列的操作实现代码如下：

  /**
     * 从数组创建优先级队列
     */
    PQ *newPQ(int A[], int n)
    {
        PQ *pq = (PQ *)malloc(sizeof(PQ) + sizeof(int) * n);
        pq->size = 0;
        pq->capacity = n;
    
        int i;
        for (i = 0; i < pq->capacity; i++) {
            pq->elems[i] = A[i];
            pq->size++;
        }
        buildMaxHeap(pq->elems, pq->size);
    
        return pq;
    }
    
    int maximum(PQ *pq)
    {
        return pq->elems[0];
    }
    
    int extractMax(PQ *pq)
    {
        int max = pq->elems[0];
        pq->elems[0] = pq->elems[--pq->size];
        maxHeapify(pq->elems, 0, pq->size);
        return max;
    }
    
    PQ *insert(PQ *pq, int key)
    {
        int newSize = ++pq->size;
        if (newSize > pq->capacity) {
            pq->capacity = newSize * 2;
            pq = (PQ *)realloc(pq, sizeof(PQ) + sizeof(int) * pq->capacity);
        }
        pq->elems[newSize-1] = INT_MIN;
        increaseKey(pq, newSize-1, key);
        return pq;
    }
    
    void increaseKey(PQ *pq, int i, int key)
    {
        int *elems = pq->elems;
        elems[i] = key;
    
        while (i > 0 && elems[PARENT(i)] < elems[i]) {
            swapInt(elems, PARENT(i), i);
            i = PARENT(i);
        }
    }
    Java极客，javajike.com

参考资料

算法导论第6章《堆排序》

作者：ssjhust

来源：https://juejin.im/post/5b9e6341e51d450e51626374

阅读全文

本文为原创文章，转载请标明出处。
本文链接：http://blog.fangzhipeng.com/javainterview/2019/06/25/erchadui.html
本文出自方志朋的博客

（转载本站文章请注明作者和出处方志朋-forezp）

1 数据结构和算法面试题系列—二叉堆