八大排序算法
一、直接插入 - 1.基本思路 - 2.代码实现 - 3.时间复杂度和空间复杂度
二、希尔排序 - 1.基本思路 - 2.代码实现 - 3.时间复杂度和空间复杂度
三、简单选择 - 1.基本思路 - 2.代码实现 - 3.时间复杂度和空间复杂度
四、堆排序 - 1.基本思路 - 2.代码实现 - 3.时间复杂度和空间复杂度
五、冒泡排序 - 1.基本思路 - 2.代码实现 - 3.时间复杂度和空间复杂度
六、快速排序 - 1.基本思路 - 2.代码实现 - 3.时间复杂度和空间复杂度
七、归并排序 - 1.基本思路 - 2.代码实现 - 3.时间复杂度和空间复杂度
八、基数排序 - 1.基本思路 - 2.代码实现 - 3.时间复杂度和空间复杂度
总结

八大排序算法

一、直接插入

1.基本思路

在要排序的一组数中，假设前面(n-1) [n>=2] 个数已经是排好顺序的，现在要把第n个数插到前面的有序数中，使得这n个数也是排好顺序的。如此反复循环，直到全部排好顺序。

2.代码实现

1.遍历数组，每次循环从第二个数字往前插入
2.设定插入数和得到已经排好序列的最后一个数的位数。temp和j=i-1。
3.从最后一个数开始向前循环，如果插入数小于当前数，就将当前数向后移动一位。

public static void insertSort(int[] data) {
    int temp;
    for(int i = 1;i < data.length; i++){// 取第i个数,插入前边的有序的序列
        temp = data[i];
        int j;
        for(j = i - 1; j>=0; j--) {// 从第i-1的位置上开始比较
            if(data[j] > temp) {// 若前面的数大，则往后挪一位
                data[j+1] = data[j];
            } else {
                break;// 否则，说明要插入的数比较大
            }
        }
        data[j+1] = temp;// 找到这个位置，插入数据
    }
}

3.时间复杂度和空间复杂度

直接插入排序的平均复杂度为O(n²)，最坏时间复杂度：O(n²)，空间复杂度：O(1)，没有分配内存。

二、希尔排序

针对直接插入排序下的效率问题，有人对此进行了改进与升级，这就是现在的希尔排序。希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。

1.基本思路

1.数的个数为length，i=length/2，将下标差值为i的数分为一组，构成有序序列。
2.再取i=i/2 ，将下标差值为i的数分为一组，构成有序序列。
3.重复第二步，直到k=1执行简单插入排序。

思路：

1.希尔排序（shell sort）这个排序方法又称为缩小增量排序，是1959年D·L·Shell提出来的。该方法的基本思想是：设待排序元素序列有n个元素，首先取一个整数increment（小于n）作为间隔将全部元素分为increment个子序列，所有距离为increment的元素放在同一个子序列中，在每一个子序列中分别实行直接插入排序。然后缩小间隔increment，重复上述子序列划分和排序工作。直到最后取increment=1，将所有元素放在同一个子序列中排序为止。
2.由于开始时，increment的取值较大，每个子序列中的元素较少，排序速度较快，到排序后期increment取值逐渐变小，子序列中元素个数逐渐增多，但由于前面工作的基础，大多数元素已经基本有序，所以排序速度仍然很快。

希尔排序举例：

2.代码实现

1.遍历数组，每次循环从第二个数字往前插入
2.设定插入数和得到已经排好序列的最后一个数的位数。temp和j=i-1。
3.从最后一个数开始向前循环，如果插入数小于当前数，就将当前数向后移动一位。

（1）首先确定每一组序列的下标的间隔，循环每次需要的间隔：int i = length/2; i >0 ; i /= 2

（2）然后将每一组序列中元素进行插入排序，第二组第一个插入的数字是第一组第一个插入数字之后的那个数组，从i之后每个数字都要进行插入排序，就是插入的序列是各自不同的序列，不是一个一个子序列循环，而是在一个循环中for (int j=i;j<length;j++)完成所有子序列的插入排序。

（3）直到i=0为止。

public static void shellSort(int[] array) {
    int length = array.length;
    for (int i = length / 2; i > 0; i /= 2) {//序列的间隔，一直到间隔为一，这时候就只有一个子序列
        for (int j = i; j < length; j++) {//从i之后每个数字都要进行插入排序，就是插入的序列是各自不同的序列
            int temp = array[j];//里面就是直接插入算法
            int k;
            for (k = j - i; k >= 0; k -= i) {//实现各个数字插入排序到不同的序列中，直到间隔为1的时候，只有一个序列，就是完全的一个直接插入排序
                if (temp < array[k]) {
                    array[k + i] = array[k];
                } else {
                    break;
                }
            }
            array[k + i] = temp;//把数字插入到位置上
        }
    }
    System.out.println(Arrays.toString(array));
}

3.时间复杂度和空间复杂度

希尔排序的平均时间复杂度为O(n²)，空间复杂度O(1) 。

三、简单选择

1.基本思路

基本原理如下：对于给定的一组记录，经过第一轮比较后得到最小的记录，然后将该记录的位置与第一个记录的位置交换；接着对不包括第一个记录以外的其他记录进行第二次比较，得到最小记录并与第二个位置记录交换；重复该过程，直到进行比较的记录只剩下一个为止。

2.代码实现

1.确定要插入最小值的位置，从0开始到最后int i = 0; i <len ; i++
2.将每次开始位置上的数字暂定为最小值min,从开始数字之后一个个和min比较，再把最小值存放到min
3.将最小值所在位置上的数字和开始位置上的数字交换

public static void selectSort(int[] array) {
    int len = array.length;
    for (int i = 0; i < len; i++) {//确定每次开始的位置
        int min = array[i];//设定开始数字为最小的值最小值
        int flag = i;
        for (int j = i + 1; j < len; j++) {//把最小值存放到min,从开始数字向后一个个和min比较，再把最小值存放到min
            if (min > array[j]) {
                min = array[j];
                flag = j;
            }
        }
        if (flag != i) {
            array[flag] = array[i];
            array[i] = min;
        }
    }
    System.out.println(Arrays.toString(array));
}

3.时间复杂度和空间复杂度

简单选择排序的时间复杂度为O(n²)

四、堆排序

1.基本思路

1.若array[0，…，n-1]表示一颗完全二叉树的顺序存储模式，则双亲节点指针和孩子结点指针之间的内在关系如下：

任意一节点指针 i：
父节点：i==0 ? null : (i-1)/2
左孩子：2*i + 1
右孩子：2*i + 2

2.堆得定义

n个关键字序列array[0，...，n-1]，当且仅当满足下列要求：(0 <= i <= (n-1)/2)
① array[i] <= array[2*i + 1] 且 array[i] <= array[2*i + 2]； 称为小根堆；
② array[i] >= array[2*i + 1] 且 array[i] >= array[2*i + 2]； 称为大根堆；

3.建立大顶堆

n个节点的完全二叉树array[0，…，n-1]，最后一个节点n-1是第(n-1-1)/2个节点的孩子。对第(n-1-1)/2个节点为根的子树调整，使该子树称为堆。

对于大根堆，调整方法为：若【根节点的关键字】小于【左右子女中关键字较大者】，则交换。

之后向前依次对各节点（(n-2)/2 - 1）~ 0为根的子树进行调整，看该节点值是否大于其左右子节点的值，若不是，将左右子节点中较大值与之交换，交换后可能会破坏下一级堆，于是继续采用上述方法构建下一级的堆，直到以该节点为根的子树构成堆为止。

反复利用上述调整堆的方法建堆，直到根节点。

4.堆排序（大顶堆）

①将存放在array[0，...，n-1]中的n个元素建成初始堆；
②将堆顶元素与堆底元素进行交换，则序列的最大值即已放到正确的位置；
③将数组中array[0，...，n-1]前n-1个元素再次形成大根堆，再重复第②③步，直到堆中仅剩下一个元素为止。

2.代码实现

/**
    *  大顶堆排序
    * @param array
    */
public static void maxHeapSort(int[] array) {
    int i;
    int len = array.length;
    // 构建大顶堆
    for (i = len / 2 - 1; i >= 0; i--) {
        adjustMaxHeap(array, i, len);
    }
    // 堆顶是最大值，交换堆顶和最后一个数，再重新调整最大堆，下一次循环   i--
    for (i = len - 1; i >= 0; i--) {
        int temp = array[0];
        array[0] = array[i];
        array[i] = temp;
        adjustMaxHeap(array, 0, i);
    }
    System.out.println(Arrays.toString(array));
}
private static void adjustMaxHeap(int[] a, int pos, int len) {
    int temp;
    int child;
    for (temp = a[pos]; 2 * pos + 1 < len; pos = child) {
        // 数组从0开始，r(i)>=r(2i) r(i)>=r(2i+1)  对应 pos => 2 * pos + 1 和 2 * pos +2
        child = 2 * pos + 1;
        // 有右孩子，且右孩子数值更大
        if (child + 1 < len && a[child] < a[child + 1]) {
            child++;
        }
        // 最大的孩子大于根节点
        if (a[child] > temp) {
            a[pos] = a[child];
        } else {
            break;
        }
    }
    a[pos] = temp;
}

3.时间复杂度和空间复杂度

时间复杂度:建堆：o(n)，每次调整o(log n)，故最好、最坏、平均情况下：o(n*logn);

五、冒泡排序

1.基本思路

一次冒泡将序列中从头到尾所有元素两两比较，将最大的放在最后面。

将剩余序列中所有元素再次两两比较，将最大的放在最后面。

重复第二步，直到只剩下一个数。

2.代码实现

/**
 * @author fupeng
 * 冒泡排序优化第二版
 * 第一版优化增加flag标记，没有数字交换直接return，最优时间复杂度O(n)
 * 第二版优化，增加tempPostion记录内循环最后一次交换的位置，来缩减内循环的次数
 */
public static void bubbleSort(int[] array) {
    int len = array.length - 1;
    // 开辟一个临时空间, 存放交换的中间值
    int temp;
    // 记录最后一次交换的位置
    int tempPostion = 0;
    // 要遍历的次数
    for (int i = 0; i < array.length - 1; i++) {
        int flag = 1; // 设置一个标志位
        // 依次比较相邻两个数的大小，遍历一次后，会将前面没有排好序的最大值放到后面位置
        for (int j = 0; j < len; j++) {
            // 比较相邻的元素，如果前面的数大于后面的数，交换
            if (array[j] > array[j + 1]) {
                temp = array[j + 1];
                array[j + 1] = array[j];
                array[j] = temp;
                // 发生交换，标志位置0
                flag = 0;
                // 记录交换的位置
                tempPostion = j;
            }
        }
        // 把最后一次交换的位置给len，来缩减内循环的次数
        len = tempPostion;
        // 如果没有交换过元素，则已经有序
        if (flag == 1) {
            System.out.println(Arrays.toString(array));
            return;
        }
    }
    System.out.println(Arrays.toString(array));
}

3.时间复杂度和空间复杂度

冒泡排序的最好时间复杂度为O(n),最坏时间复杂度为O(n²),平均时间复杂度为O(n²),空间复杂度为O(1),它是一种稳定的排序算法。

六、快速排序

1.基本思路

快速排序使用分治策略来把一个序列（list）分为两个子序列（sub-lists）。步骤为：

1.从数列中挑出一个元素，称为”基准”（pivot）。
2.重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
3.递归地（recursively）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归到最底部时，数列的大小是零或一，也就是已经排序好了。这个算法一定会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

2.代码实现

public static void quickSort(int[] array) {
    sort(array, 0, array.length - 1);
    System.out.println(Arrays.toString(array));
}
private static void sort(int[] a, int low, int high) {
    int i = low;
    int j = high;
    if (a.length <= 1) {
        return;
    }
    if (i >= j) {
        return;
    }
    int index = a[i];
    while (i < j) {
        while (i < j && a[j] >= index)
            j--;
        if (a[j] < index)
            a[i++] = a[j];
        while (i < j && a[i] <= index)
            i++;
        if (a[i] > index)
            a[j--] = a[i];
    }
    a[i] = index;
    sort(a, low, i - 1);
    sort(a, i + 1, high);
}

3.时间复杂度和空间复杂度

虽然快排的时间复杂度达到了 O(n²)，但是在大多数情况下都比平均时间复杂度为 O(n logn) 的排序算法表现要更好。

七、归并排序

1.基本思路

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案”修补”在一起，即分而治之)。

1.分而治之

可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。

2.合并相邻有序子序列再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

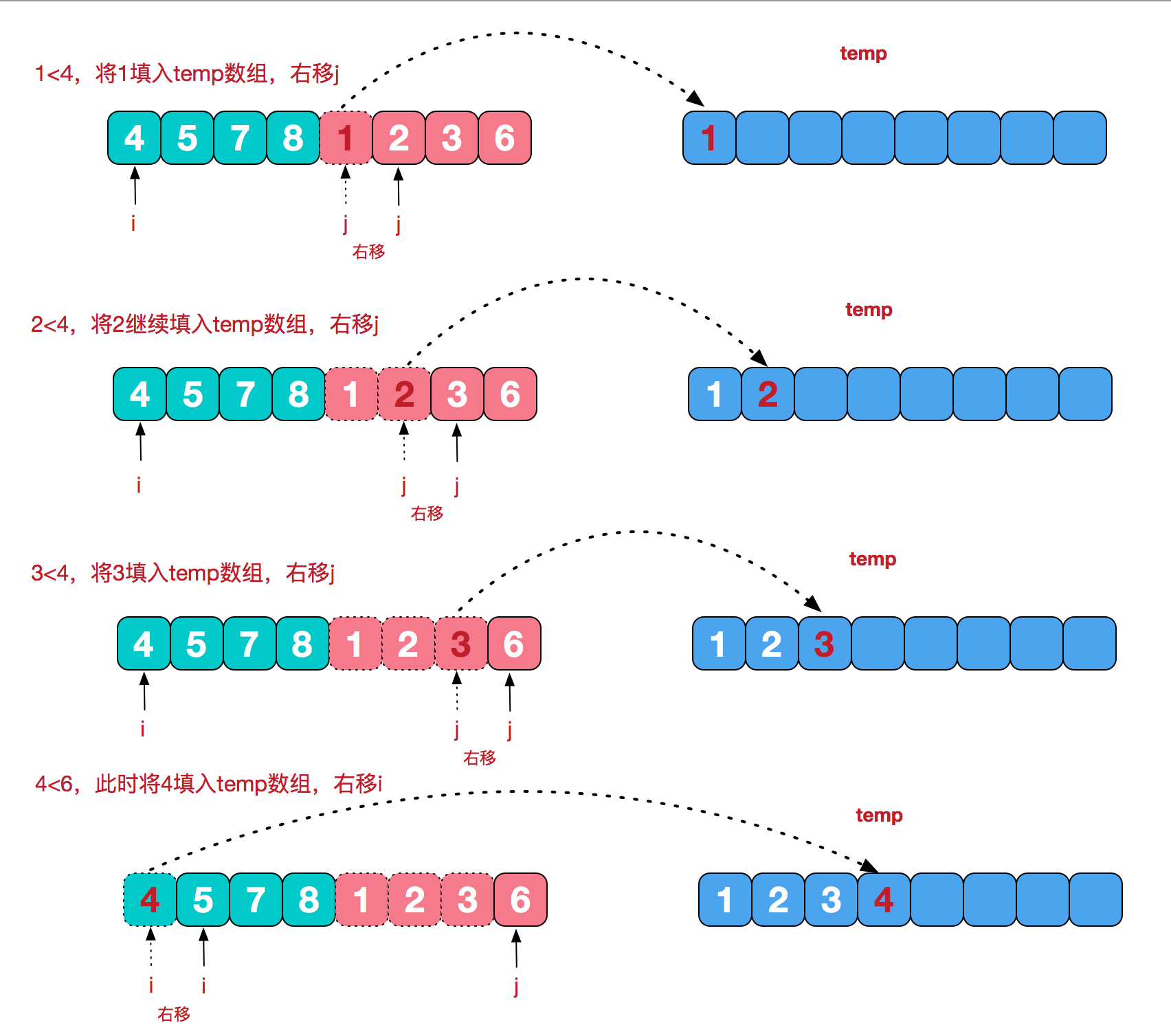
2.代码实现

public static void mergeSort(int[] array) {
    int[] temp = new int[array.length];// 在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
    mergeSort(array, 0, array.length-1, temp);
    System.out.println(Arrays.toString(array));
}
private static void mergeSort(int[] arr, int left, int right, int []temp) {
    if(left < right) {
        int mid = (left+right) / 2;
        mergeSort(arr, left, mid, temp);// 左边归并排序，使得左子序列有序
        mergeSort(arr, mid+1, right, temp);// 右边归并排序，使得右子序列有序
        merge(arr, left, mid, right, temp);// 将两个有序子数组合并操作
    }
}
private static void merge(int[] arr, int left, int mid, int right, int[] temp) {
    int i = left;// 左序列指针
    int j = mid+1;// 右序列指针
    int t = 0;// 临时数组指针
    while (i <= mid && j <= right) {
        if(arr[i] <= arr[j]) {
            temp[t++] = arr[i++];
        } else {
            temp[t++] = arr[j++];
        }
    }
    while(i <= mid) {// 将左边剩余元素填充进temp中
        temp[t++] = arr[i++];
    }
    while(j <= right) {// 将右序列剩余元素填充进temp中
        temp[t++] = arr[j++];
    }
    t = 0;
    // 将temp中的元素全部拷贝到原数组中
    while(left <= right) {
        arr[left++] = temp[t++];
    }
}

3.时间复杂度和空间复杂度

归并排序是稳定排序，它也是一种十分高效的排序，能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了一种名为TimSort的排序算法，就是归并排序的优化版本。从上文的图中可看出，每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为

log2n

。总的平均时间复杂度为O(nlogn)。而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。

八、基数排序

1.基本思路

1.基数排序的思想就是先排好各位，然后排好各位的基础上排十位，以此类推，直到遍历最高位次，排序结束（仔细理解最后一句话）
2.基数排序不是比较排序，而是通过分配和收集的过程来实现排序
3.初始化10个桶(固定的)，桶下标为0-9
4.通过得到待排序数字的个十百等位的数字，把这个数字对应的item放到对应的桶中
5.基数排序有两种排序方式：LSD和MSD，最小位优先(从右边开始)和最大位优先(从左边开始)

2.代码实现

public static void radixSort(int[] array) {
    ArrayList<ArrayList<Integer>> queue = new ArrayList<>();
    for (int i = 0; i <10 ; i++) {
        queue.add(new ArrayList<>());// 创建一个基数从0---9 每个数字上都是一个list
    }
    // 找到最大值，并判断最大值是几位数
    int max = array[0];
    for (int i = 1; i < array.length; i++) {
        if (max < array[i]) {
            max = array[i];
        }
    }
    int time = 0;
    while (max > 0) {
        max /= 10;
        time++;
    }
    for (int i = 0; i < time; i++) {// 循环每一个位数（个位、十位、百位）
        for (int j = 0; j < array.length; j++) {// 循环数组，取每一个值
            int x = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
            ArrayList<Integer> queue3 = queue.get(x);
            queue3.add(array[j]);
            queue.set(x, queue3);
        }
        int count = 0;
        for (int k = 0; k < 10; k++) {
            while (queue.get(k).size() > 0) {
                ArrayList<Integer> queue4 = queue.get(k);
                array[count] = queue4.get(0);
                queue4.remove(0);
                count++;
            }
        }
    }
}

3.时间复杂度和空间复杂度

log2n

。总的平均时间复杂度为O(nlogn)。而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。

总结

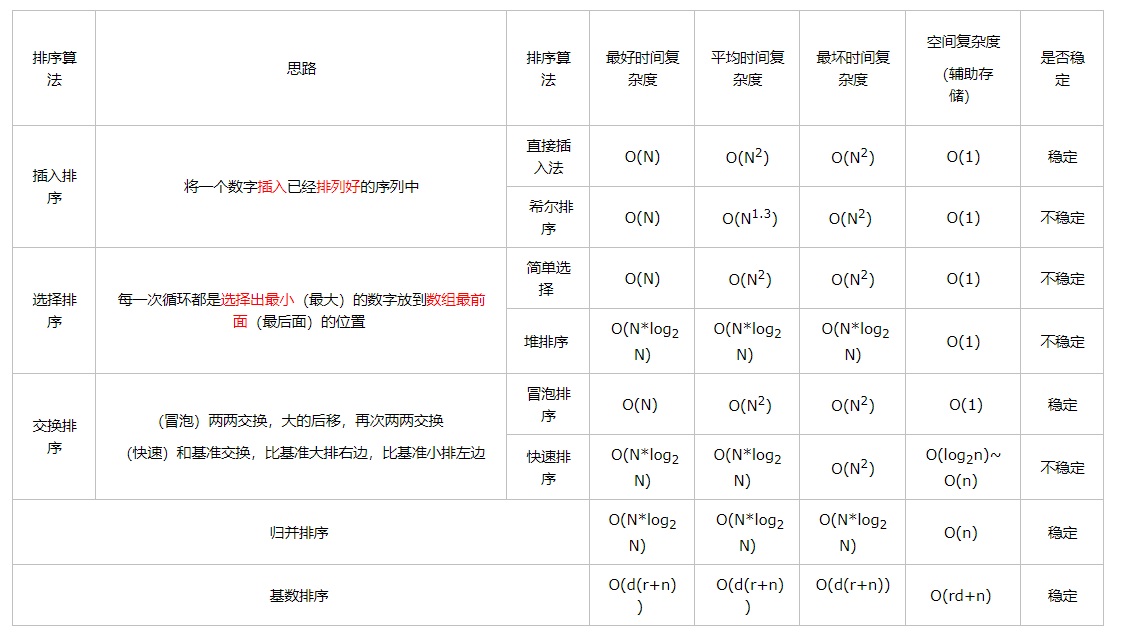
引用：

https://www.cnblogs.com/mensan/p/10570050.html

https://www.cnblogs.com/jyroy/p/11248691.html

https://www.cnblogs.com/chengxiao/p/6194356.html

https://www.jianshu.com/p/8340dfaea3af

作者： _yosemite

来源：https://blog.csdn.net/godloveleo9527/article/details/106816989?utm_medium=distribute.pc_feed.none-task-blog-personrec_tag-18.nonecase&dist_request_id=1328769.70815.16176945767498397&depth_1-utm_source=distribute.pc_feed.none-task-blog-personrec_tag-18.nonecase

阅读全文

本文为原创文章，转载请标明出处。
本文链接：http://blog.fangzhipeng.com/javainterview/2019/06/25/8dpx.html
本文出自方志朋的博客

（转载本站文章请注明作者和出处方志朋-forezp）

八大快速排序

八大排序算法

一、直接插入

1.基本思路

2.代码实现

3.时间复杂度和空间复杂度

二、希尔排序

1.基本思路

2.代码实现

3.时间复杂度和空间复杂度

三、简单选择

1.基本思路

2.代码实现

3.时间复杂度和空间复杂度

四、堆排序

1.基本思路

2.代码实现

3.时间复杂度和空间复杂度

五、冒泡排序

1.基本思路

2.代码实现

3.时间复杂度和空间复杂度

六、快速排序

1.基本思路

2.代码实现

3.时间复杂度和空间复杂度

七、归并排序

1.基本思路

2.代码实现

3.时间复杂度和空间复杂度

八、基数排序

1.基本思路

2.代码实现

3.时间复杂度和空间复杂度

总结

宝剑锋从磨砺出，梅花香自苦寒来，用心分享，一起成长，做有温度的攻城狮!

Post Directory